Origami de Árvore de Natal | Origami
O
Natal está chegando e fazer uma árvore de natal em
origami é bem legal. Pesquisando sobre alguns modelos, encontrei uma que gostei por ter detalhes que se parecem bastante com a dos pinheiros. Infelizmente o seu autor –
Francesco Guarnieri – nos disponibilizou apenas o
Crease Pattern (CP) do seu modelo
Abete 3, mas é uma ótima oportunidade para tentarmos aprender um pouco mais sobre como decifrar o padrão de dobras. O que mostrarei aqui NÃO é um diagrama. São algumas dicas para se obter o CP, mas vocês vão perceber que ao fazer o mapa de dobras dessa forma, será fácil dobrar esta árvore de natal.
Preparativos para a Árvore de Natal
Para começar a fazer o modelo, eu preferi usar os tamanhos 7,5×7,5cm, 10x10cm, 12x12cm e 15x15cm nos quadrados para fazer os 4 octógonos – veja o texto
Como Fazer um Octógono a Partir de um Quadrado – das folhas e um octógono de 15x15cm para o caule. Isto me resultou num pinheirinho bem bacana de 11cm de altura. Para quem quiser saber o papel que usei para a da foto acima, são os da linha Origami nas cores 1010 e 1015 da Diamond Papers.
Lembrem-se que caso queiram fazer uma árvore maior, é possível fazê-la com mais módulos das folhas e ir aumentando o tamanho do quadrado. Por exemplo, no meu caso eu poderia colocar um de 18x18cm e outro de 21x21cm. E assim por diante. Reparem que se eu fizer uma árvore maior, o tamanho do caule também tem que aumentar e é sempre a do quadrado maior utilizado nas folhas. E ainda, a gramatura do papel começa a ter importância quanto maior for a árvore.
Decifrando o Crease Pattern do Caule
Olhando para o modelo do
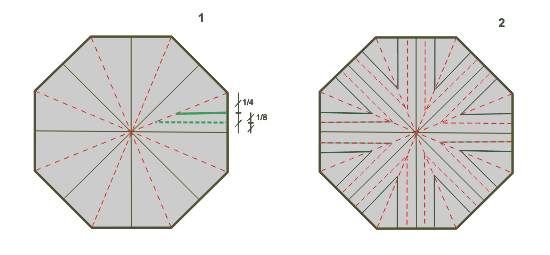
Abete 3 – clique o link que deixei – você verá que são apenas 2 octógonos apresentados. Vamos começar pelo mais simples que é o Crease Pattern do caule. Para deixar claro, a linha contínua é uma dobra montanha. A linha tracejada é uma dobra vale. As linhas preta ou vermelha são marcas já visíveis no papel. As linhas verdes são as que você ainda tem que executar.
Depois de você obter o seu octógono, você pode fazer as dobras vale que saem dos vértices – encontro de 2 lados – opostos que são algumas das diagonais do octógono. As dobras montanha são as que saem da metade do lado e vão para o lado oposto. Repare que nestas dobras, sempre fazemos com que o octógono seja dividido pela metade.
Passo 1 – para completar as dobras do caule, fazemos a dobra 1/4 do lado até atingir a diagonal. Aí fazemos a dobra 1/8, também até atingir a diagonal.
Passo 2 – agora basta repetir essas dobras por toda a volta do octógono.
Decifrando o Crease Pattern das Folhas
Antes de iniciar as dobras das folhas, você deve ter feito as mesmas dobras vale das diagonais e dobras montanhas que partem do lado. Aquelas mesmas do caule e que dividiam o seu octógono pela metade. Lembra?
Como podem perceber no CP original, as folhas possuem mais dobras diferentes, mas mesmo assim é possível “adivinhar” algumas referências. A primeira coisa que reparei foi que as dobras se iniciaram com os 2 octógonos centrais. A partir daí, foi descobrir como fazê-los.
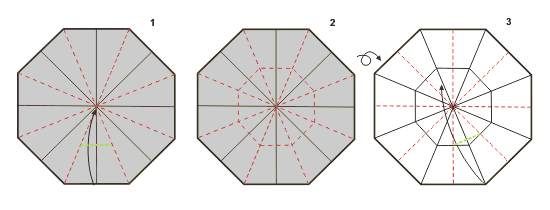
Passo 1 – o 1º octógono central a ser dobrado é levando o lado até a linha da dobra central que é paralela a esse mesmo lado. Faça essa dobra vale até atingir as dobras diagonais.
Passo 2 – repita isso com todos os outros lados e vire para o outro lado do papel. Repare que neste lado, as dobras se invertem. O que é vale do outro lado, é montanha deste lado. Isso é meio óbvio, mas sempre vale a pena lembrar.
Passo 3 – o 2º octógono central é obtido através da referência dos lados do último octógono dobrado. Repare que uma dobra diagonal cruza exatamente ao meio de cada lado. Essas são as referências para dobrarmos os lados deste 2º octógono. Vejam a figura.
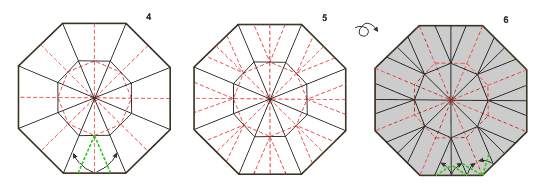
Passo 4 – agora é fazer as dobras em V a partir dos vértices deste 2º octógono. Para fazê-lo, basta fazer uma dobra vale que parte do vértice fazendo com que a marca que está na metade do lado alcance a dobra diagonal do lado direito. Essa dobra é repetida do lado esquerdo, assim teremos o V de cabeça-para-baixo.
Passo 5 – Repita isso em todos os vértices e depois vire para o outro lado. Repetindo novamente para não esquecer, o que é vale do outro lado, é montanha neste.
Passo 6 – Agora iremos usar as dobras V como referência para finalizar o CP. Basta fazer coincidir o lado do octógono até uma das dobras adjacentes. Basta reparar que quando a dobra inicia pelo lado do octógono, as dobras formam um V de cabeça-para-baixo. Quando a dobra inicia pelo vértice, forma um V normal.
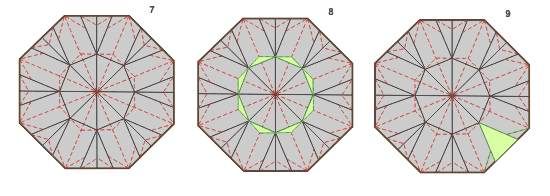
Passo 7 – repita as dobras em toda a volta do octógono e assim o CP está completo. A dobra que falta só aparecerá quando executarmos todas as dobras.
Passo 8 – a sequência para fazer a forma das folhas é efetuando as dobras dos octógonos centrais primeiro. Essas dobras farão com que o módulo fique tridimensional. A forma é parecida com a de um guarda-chuva. É um pouco difícil porque temos que fazer o papel se sobrepor.
Passo 9 – com a figura parecendo um guarda-chuva, agora basta criar suas pontas. Para tanto, é necessário executar as dobras do triângulo que está no lado e suas dobras adjacentes. Quando fizer, você reparará que os lados maiores desse triângulo ficarão unidos e as dobras adjacentes criarão uma trava. Repita o mesmo em toda a volta que você terá as pontas das folhas do pinheiro.
Ajuda em Vídeo
Se você executou todos os passos anteriores, meus parabéns. Ao tentar fazê-los, você já começou a assimilar um pouco de como decifrar um CP. Não é uma ciência exata, porque depende principalmente da experiência que você tem com o origami. E quanto mais tentar dobrá-los, mais experiência você terá para decifrar o próximo…
De qualquer forma, se você não conseguiu entender algum passo, deixo aqui o vídeo que a Sara Adams fez – por coincidência, ela publicou enquanto eu estava escrevendo este texto – mas ele só será realmente uma ajuda, se você tiver tentado dobrar o CP antes.
Como em quaquer vídeo, ter uma pessoa que faz as dobras antes, facilita muito dobrar um modelo específico, mas eles vão te deixando cada vez mais dependente de alguém para dobrar, principalmente se você for um principiante. Quebrar a cabeça faz parte de qualquer aprendizado, seja ele qual for.
Finalizando
Se você gostou de dobrar esta árvore de natal, volte ao flickr do Francesco Guarnieri e tente decifrar as dezenas de modelos que ele apresenta por lá. Um dos que recomendo é o
Fiori Geometrico que
já dobramos no Grupo Origami Beagá. Eles são uma boa diversão e um bom exercício na compreensão dos CPs.
”Ai, caramba! Minha mãe pediu para ser minha amiga no Facebook. Aceitei, né? Mas que medo de ela escrever no meu mural ‘oi, Fofuchinho’”. Ih! De fato, quem tem mãe como amiga nas redes sociais deve ficar um pouco #tenso!
Compartilhar no MySpace!
